This is a summary note of the course “Computer Organization and Architecture” by Professor William Stallings.
The remaining contents is organized as:
- Chapter 12
- Machine Instruction Characteristics
- Elements of a machine instruction
- Instruction representation
- Instruction type
- *Number of addresses
- Instruction set design
- Types of Operands
- Types of Operations
- Machine Instruction Characteristics
Chapter 12: Instruction Sets (I)
Concepts
| Name or Abbr. | Meaning | Chinese |
|---|---|---|
| Opcode | Operation Code | 操作码 |
| Operands | a number or quantity that has something done to it in a calculation. | 操作数 |
| Address Field | data storing address of operands | 地址字段 |
Elements of a machine instruction
The elements of a machine instruction are:
- Operation Code: a binary code that specifies the operation to be performed.
- Source operands reference: source operands that are involved in the operation.
- Result operands reference: result produced by the operation.
- Next instruction reference: tells the processor where to fetch the next instruction after the instruction is executed.
Source and result operands can be in memory, registers, I/O devices, or immediate values.
Here’s a diagram of a machine executing an instruction:
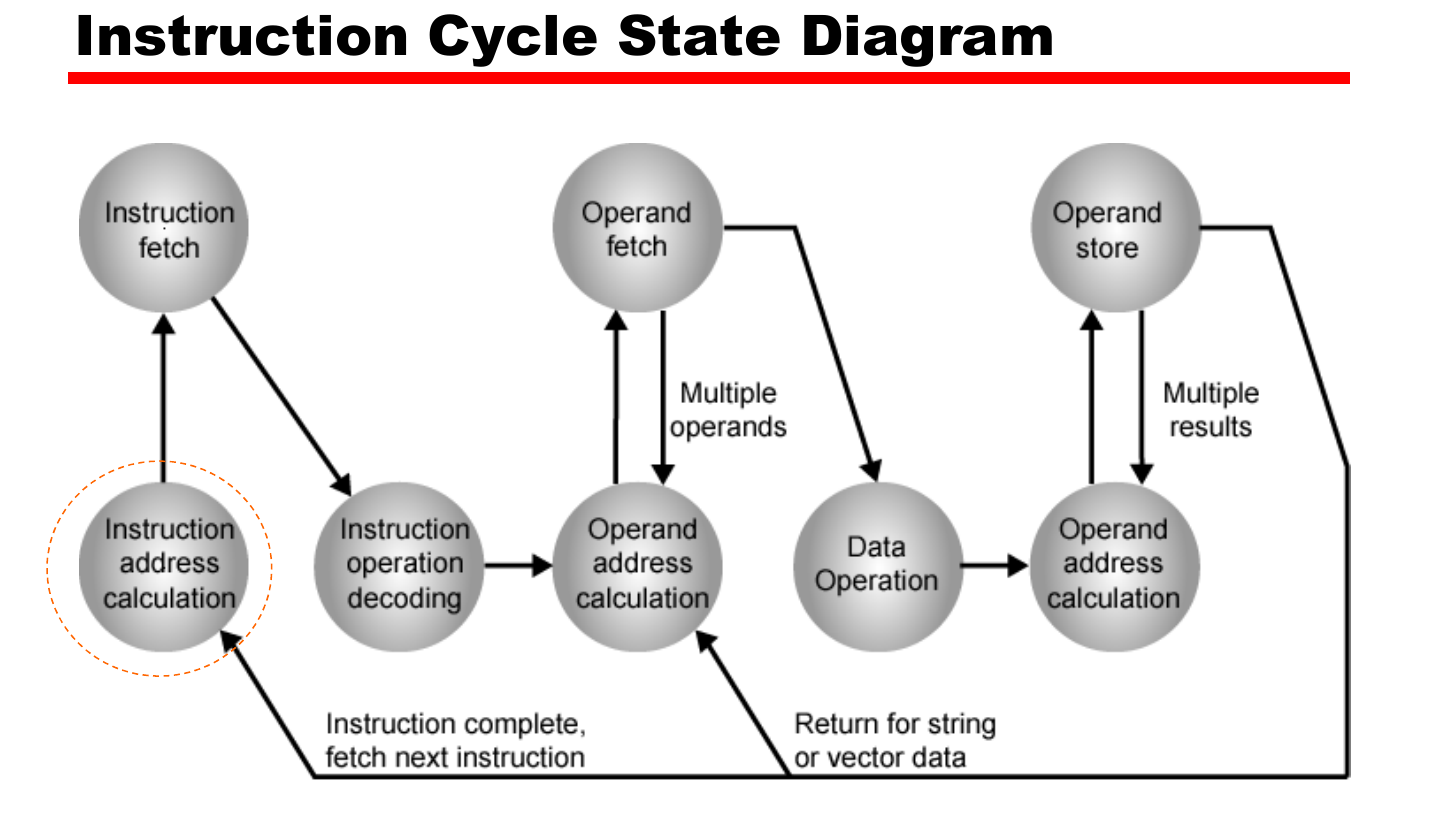
In the diagram we can find that: both the source operands and the result operands should be addressed by “Operand address calculation”.
Instruction representation
In machine code each instruction has a unique bit pattern. But for programmers each instruction has a symbolic representation, like ADD, SUB, AND, OR, etc. These symbolic representations are called mnemonics.(助记符)
Here’s a diagram of common mnemonics in IAS Structure (Mentioned in Ch1):
| Mnemonic | Operation |
|---|---|
| ADD | Addition |
| SUB | Subtraction |
| MUL | Multiplication |
| DIV | Division |
| LOAD | Load Data from memory |
| STOR | Store Data to memory |
A typical 16-bit instruction format is:
Opcode [4 bits]| Operand Reference[6 bits] | Operand Reference[6 bits]
High level languages are mostly first translated into machine code, and then it could be executed by the processor.
Some compiler can directly translate high level language into machine code, like g++ or clang, but some compilers first translate it into Assembly language and then into machine code. While languages like Python uses a explainer instead of a compiler, so it doesn’t need to be translated into machine code.这是一个坑!!
Instruction type
Like the concept of Structure Function, in Chapter 1, the instruction type can be separated into 4 categories (with Assembly instructions for example):
- Data Processing: Arithmetic and logic instructions. (ADD, SUB, AND, OR, etc.)
- Data Storage: Movement of data into or out of register and or memory locations.(MOV, STO, LOD, etc.)
- Data Movement: I/O instructions. (IN, OUT, etc.)
- Control: Test and branch instructions. (JMP, JC, etc.)
Number of addresses
Four types of numbers of addresses: 3,2,1,0.
More addresses means more complex instructions, more registers, but less instructions in a program. Fewer addresses means less complex instructions and faster fetch/execution of instructions but more instructions in a program.
3-address instructions
Two sources and one result address included in the instruction. However it’s not common because it needs long instruction format.
Symbolic representation:
OP A,B,C <-> A <- B OP C
2-address instructions
Compared to 3-address instructions, 2-address instructions only need one source and one address for operand + result (Multiplexing). Classical examples are:
- MOV: Move data from one location to another.
- ADD: Add two numbers and store the result in a register or memory location.
- SUB: Subtract two numbers and store the result in a register or memory location.
Symbolic representation:
OP A,B <-> A <- A OP B
1-address instructions
Only one address included in the instruction. The second address is implicit. Usually used as:
LOAD A <-> AC <- A
It is usually a register or accumulator to hold an 1-address instruction.
0-address instructions
Use a stack to find the operands. See the example of c=a-b below:
push a
push b
sub ; pop a and b from stack and add them, push the result to stack
pop c
The operation command find the operands from the top of the stack. And the first operand is below the second operand.
Instruction set design
Repertoire means a list or supply of capabilities.
Fundamental Issues:
- Operation repertoire: System provide how many and which operations?
- Data types
- Instruction Format: Length, Number of Addresses, etc.
- Registers: Number of used registers
- Addressing: Addressing Mode
Types of Operands
| Catagory | Includes | Notes |
|---|---|---|
| Addresses | Unsigned Int , with various Address Modes |
/ |
| Numbers | Binary FxP or Int, Binary Float, Packed Decimal |
/ |
| Characters | IRA (International Reference Alphabet), 7-bit representation for each character, and EBCDIC in IBM main frames |
compatible with packed decimal |
| Logical Data | 1-bit items or flags |
Each addressable unit is seperated as n 1-bit items |
Types of Operations
The type of operation is referred to opcode. The types are all included in x86 systems, so that we can refer to classical operations in x86 systems.
| Catagory | Function | Notes | Typical operations |
|---|---|---|---|
| Data Transfer | Transfer data from src to dst | May be different instructions for different movements or one instruction for different addresses | MOV |
| Arithmetic | Basic Calculations for catagories of numbers |
Include data transfer | ADD, SUB, MUL, DIV |
| Logical | Bitwise logical operations | Distinguish Logical Shift (Put a 0 in array), Arithmetic Shift (Most significant sign bit is perserved), and Rotate | AND, NOT, XOR, OR |
| Conversion (转换) | Convert a data type to another (mostly in the same catagory) | / | AAA |
| I/O | Control of I/O Port | Specific instructions, or using I/O processor, or memory mapped programmed I/O, or DMA | IN, OUT |
| System Control | Operations that can be only executed in privileged state | Mostly reserved for system | Alter a control register |
| Transfer of Control | Change the sequence of instruction | (Conditional) Branches, Skips, Procedure call | JMP, JNZ |
Branches, Skips and Procedures
For unconditional branch, the branch will be always taken, and the execution will be ended at CO stage. For conditional branch, the branch will be taken only if the condition is satisfied. To generate a condition, we can either use condition code or use a three-address instruction like CMP.
For skips, the next instruction will be skipped if condition is satisfied.
For a procedure, it can be called from more than one location, i.e. reentrant procedure, and allows nesting(嵌套). However each procedure call requires a return. The return address are stored at:
- Register
- Top of a stack
- or the start place of called procedure.
Endian
- Big Endian: Most significant byte at the lowest address in memory, stack, etc.
- Little Endian: Least significant byte at the lowest address in memory, stack, etc.
Reverse Polish
Reverse Polish notation (RPN), also known as reverse Łukasiewicz notation, Polish postfix notation or simply postfix notation, is a mathematical notation in which operators follow their operands, in contrast to prefix or Polish notation (PN), in which operators precede their operands. The notation does not need any parentheses for as long as each operator has a fixed number of operands.
Questions
Question 12.6:

Answer:
- For zero address instructions:
PUSH B
PUSH C
MUL
PUSH A
ADD
PUSH D
PUSH E
PUSH F
MUL
SUB
DIV
- For one address instructions:
LOAD B ; Load B into register
MUL C
STORE TEMP1 ; Store the result of multiplication in TEMP1 register
LOAD A
ADD TEMP1
STORE TEMP2
LOAD E
MUL F
STORE TEMP3
LOAD D
SUB TEMP3
STORE TEMP4
LOAD TEMP2
DIV TEMP4
STORE RESULT
- For two address instructions:
MOVE R1, B ; Load B into reg R1
MUL R1, C ; R1 = B * C
MOV R2, A ; Load A into reg R2
ADD R2, R1 ; R2 = A + (B * C)
MOVE R3, E
MUL R3, F ; R3 = E * F
MOVE R4, D
SUB R4, R3 ; R4 = D - (E * F)
DIV R2, R4 ; R2 = (A + B * C) / (D - E * F)
MOVE RESULT, R2
- For three address instructions:
MUL R1, B, C ; R1 = B * C
ADD R2, A, R1 ; R2 = A + (B * C)
MUL R3, E, F ; R3 = E * F
SUB R4, D, R3 ; R4 = D - (E * F)
DIV RESULT, R2, R4 ; RESULT = (A + B * C) / (D - E * F)
Question 12.18:

Answer:
- Question A:
((A + B) + C) * D - Question B:
A / B + C / D - Question C:
A / (B * C * (D + E)) - Question D:
A + B * (C + (D + E) / F - G) / H
Question 12.19:
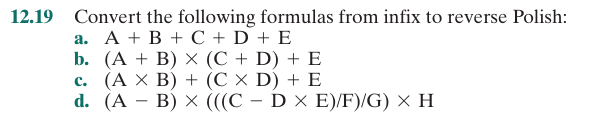
Answer:
- Question A:
A B + C + D + E + - Question B:
A B + C D + * E + - Question C:
A B * C D * + E + - Question D:
A B - C D E * - F / G / * H *
Note: Reverse Polish Expressions are not unique.