This is a summary note of the course “Computer Organization and Architecture” by Professor William Stallings.

The remaining contents is organized as:

• Chapter 4 (Pt. II)
  • Elements of Cache Design
    • Cache Addresses
    • Cache Size
    • Mapping Function
    • Replacement Algorithm
    • Write Policy
    • Line/Block Size
    • Number of Caches

---

Chapter 4 (Part II): Cache

Cache Memory Principles

Cache Memory

Why we need caches?

Caches are designed to combine the memory access time of expensive, high-speed memory combined with the large memory size of less expensive, lower-speed memory.

• A typical Organization of a three-level cache memory:
  
  

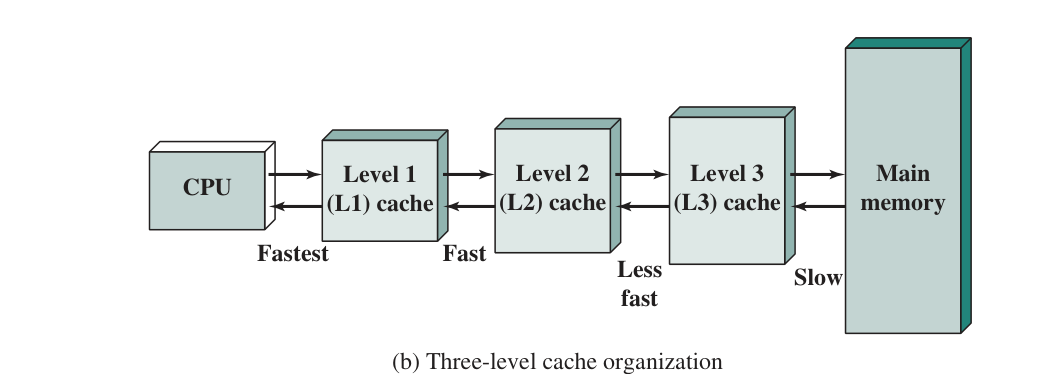
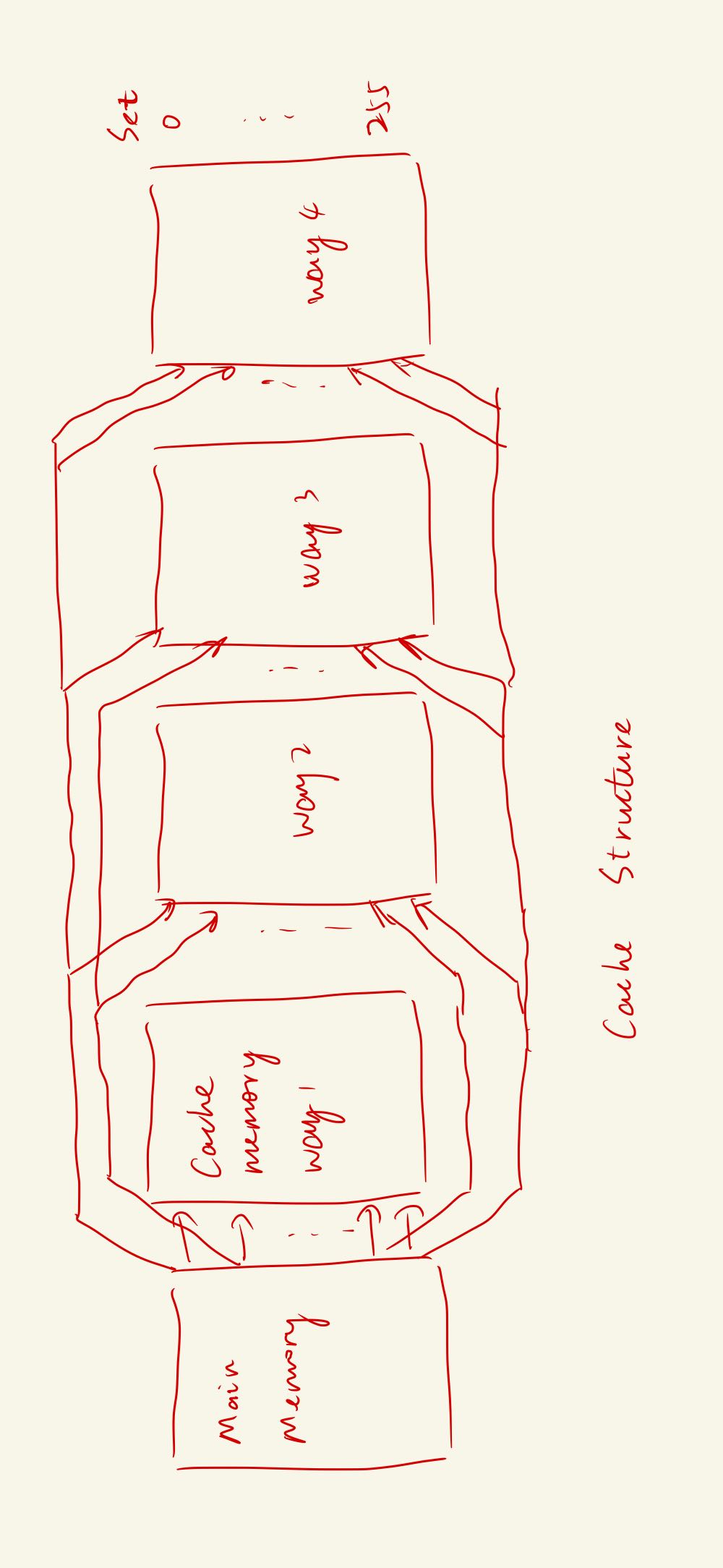
• A Cache Structure

Including multiple lines, each with a tag followed by a block. A block contains K words, where K is the Block Length. The cache is organized as a set of N cache blocks, where N is the number of lines.

Each line includes a tag that identifies which particular block is currently being stored, because the main memory stores considerbly more blocks than a cache. It also includes some hidden control bits. When we say a line size, it refers to the total number of bits in a line,NOT including the tag and control bits.

We will specify s as the length of the tag and line, r as the line size, and w as the bits of the word.

Reading process of a CPU throught a cache

RA refers to reading address.

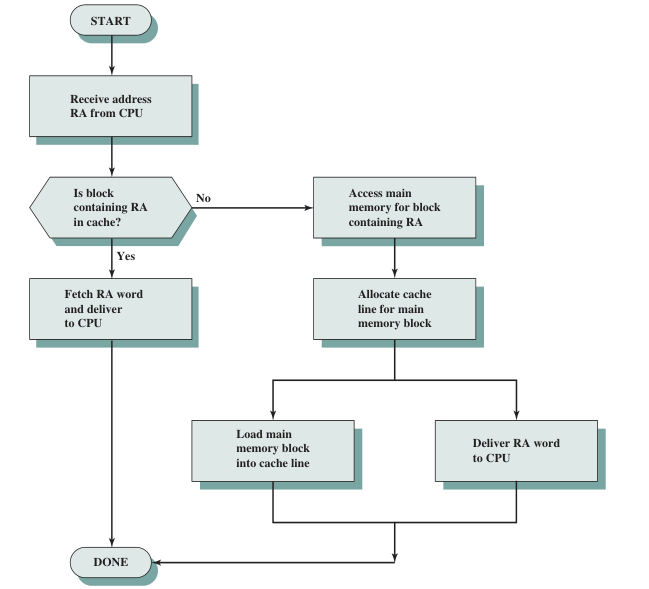
Cache Addresses

There are some concepts:

1. Virtual Memory: Virtual memory is a technique that allows programs to run without running out of physical memory. It works by mapping the virtual memory addresses to physical memory addresses.
2. Hardware Memory Management Unit (MMU): The MMU is a hardware device that translates virtual memory addresses to physical memory addresses. It is inserted between Processor and Main Memory.
3. Logical Cache is located between the MMU and the processor.
4. Physical Cache is located between the MMU and the main memory.

Cache Size

We would like the size of the cache to be small enough so that the overall average cost per bit is close to that of main memory alone and large enough so that the overall average access time is close to that of the cache alone.

Mapping Function

a means is needed for determining which main memory block currently occupies a cache line. The choice of the mapping function dictates how the cache is organized.

So there are three main mapping functions:

DIRECT MAPPING:

Each block in main memory is mapped to a single cache line.

The corresponding way is:

\[i = j \, mod \,m\]

where m is the number of cache lines and j is the main memory block number. Here is an example:

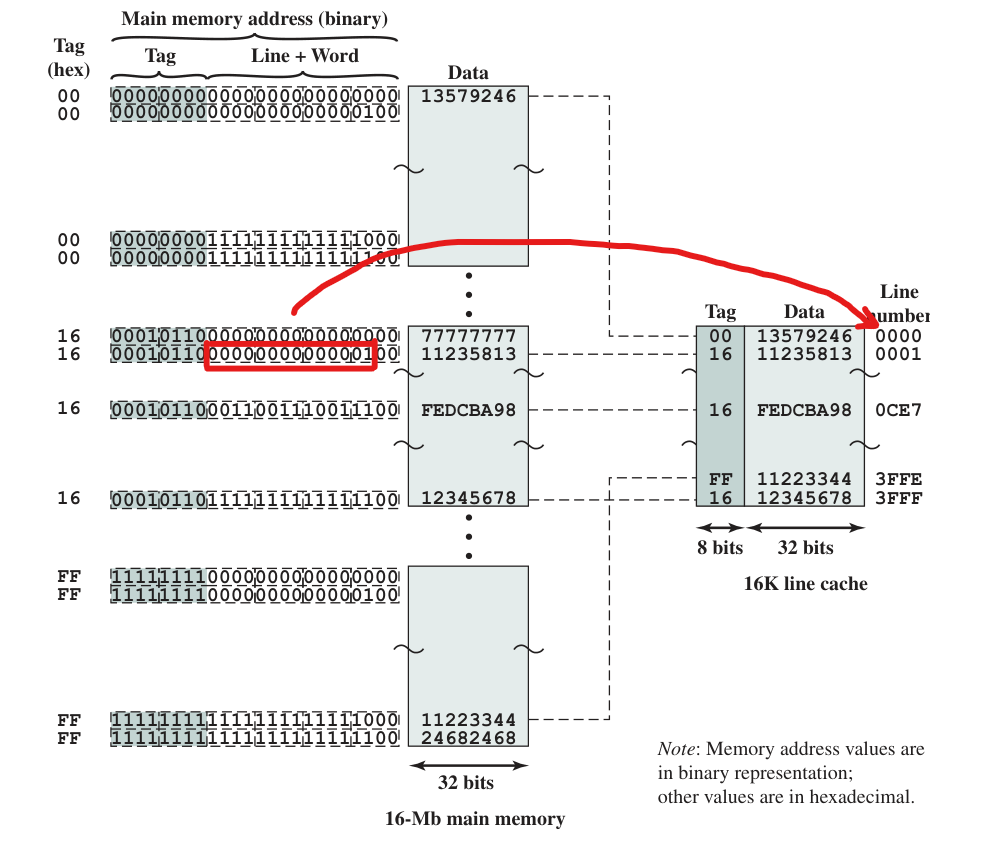
Why to store tag in the cache: When a block is actually read into its assigned line, it is necessary to tag the data to distinguish it from other blocks that can fit into that line.

There are some figures to remember. Note that we will specify s as the length of the tag and line, r as the line size, and w as the bits of the word.

1. Address length = (s+w) bits, where the most significant s bits specify a memory block, while the least significant w bits specify a word within the block.
2. Number of addressable units = \(2^{s+w}\) words. （可寻址单元）
3. Block size = Line size = \(2^w\) words.（因为是直接映射，故肯定是相同的）
4. Number of blocks in main memory = \(2^{s}\).
5. Number of cache lines = m = \(2^r\).
6. size of tag = s-r bits.

Pros and Cons:

• Pros:Very easy to implement
• Cons:fixed cache location for any given block. Thus, when two blocks are mapped to the same cache line, they will be evicted together.

ASSOCIATIVE MAPPING

Each block in main memory is permitted to be mapped to ANY cache line.

It overcomes the disadvantage of direct mapping by permitting each main memory block to be loaded into any line of the cache. In this way, a main memory address can be interpreted as only tag and word.

• Now the main memory address is divided into 22 bits of tag and 2 bits of word. by cache control logic.

There are some figures to remember. Note that we will specify s as the length of the tag and line, r as the line size, and w as the bits of the word.

1. Address length = (s+w) bits, where the most significant s bits specify a memory block, while the least significant w bits specify a word within the block.
2. Number of addressable units = \(2^{s+w}\) words. （可寻址单元）
3. Block size = Line size = \(2^w\) words.（因为是直接映射，故肯定是相同的）
4. Number of blocks in main memory = \(2^{s}\).
5. Number of cache lines = m = \(2^r\) UNDETERMINED.
6. size of tag = s bits.

• Pros:

  SET-ASSOCIATIVE MAPPING:

A Compromise between Direct and Associative Mapping. The cache is divided to a number of sets, and the block can be mapped into any line in a particular set

Now the cache includes multiple sets consisting of multiple cache lines. The cache control logic interprets the main memory address as s-d bits of tag, d bits of set number and w bits of word.

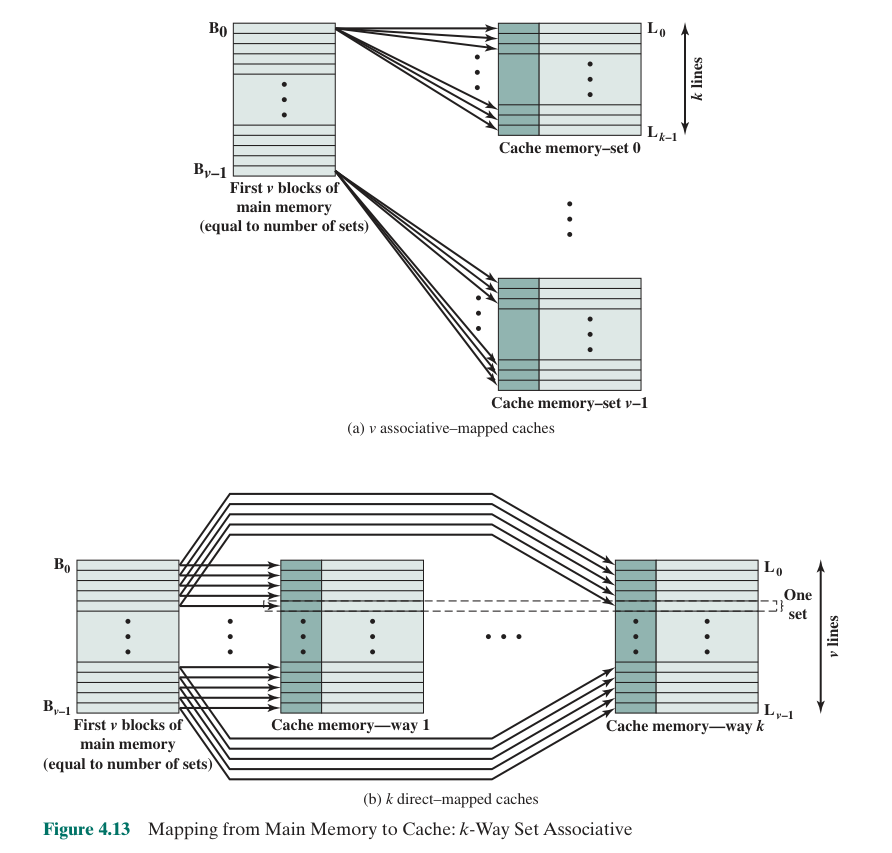
1. Address length = (s+w) bits, where the most significant s bits specify a memory block, while the least significant w bits specify a word within the block.
2. Number of addressable units = \(2^{s+w}\) words. （可寻址单元）
3. Block size = Line size = \(2^w\) words.（代表了 Main memory 中 Block 的存贮大小，进而直接对应了 Cache 中的 Line 存贮信息的大小）
4. Number of blocks in main memory = \(2^{s}\).
5. Number of cache lines = m = \(2^r\) UNDETERMINED.
6. size of tag = s bits.

• Pros: Same as Associative

Cons: Same as Associative

Review Questions

Questions

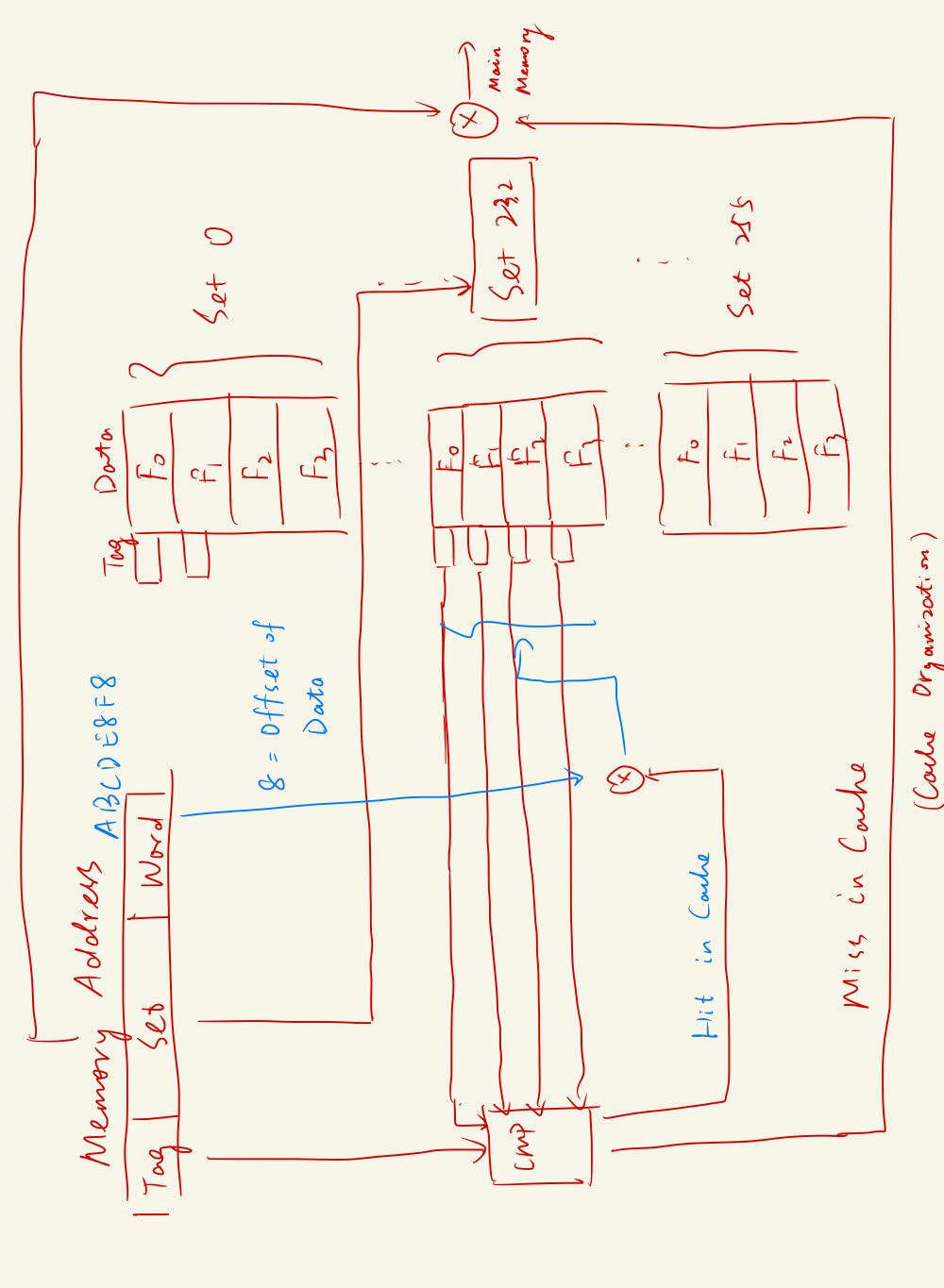
Question 4.5:Consider a 32-bit microprocessor that has an on-chip 16-kB four-way set-associative cache. Assume that the cache has a line size of four 32-bit words. Draw a block diagram of this cache showing its organization and how the different address fields are used to determine a cache hit/miss. Where in the cache is the word from memory location ABCDE8F8 mapped?

Answer: The line size is 16 bytes (4 doublewords). To address a byte in a 16-byte line, we need 4 bits for the word. There are 256 sets. To address a set, we need 8 bits for the index. The remaining bits in the 32-bit address will be used for the tag, so there are 32 − 8 − 4 = 20 tag bits.

Hex: ABCDE8F8 = 10101011110011011110 10001111 1000 (Binary).Therefore, the word from memory location ABCDE8F8 is mapped to Set 143, and within that set, it will be stored in one of the 4 lines based on the tag comparison.

Question 4.6: Given the following specifications for an external cache memory: four-way set associative; line size of two 16-bit words; able to accommodate a total of 4K 32-bit words from main memory; used with a 16-bit processor that issues 24-bit addresses. Design the cache structure with all pertinent information and show how it interprets the processor’s addresses.

Answer: Total cache size is calculated as a division of cache size and cache line size, which is 4K lines. With a four-way set associative, Number of Sets can be calculated as:

\[\frac{\text{Total Cache Lines}}{\text{Asscociativity}} = 1024 \,\text{Sets}\]

As for the 24-bit address, it is seperated into 12 bits of tag, 10 bits of set number, and 2 bits of word. Therefore, the cache structure is as same as 4.5, but with 1024 sets instead of 256 sets.

Question 4.7:The Intel 80486 has an on-chip, unified cache. It contains 8 kB and has a four-way set-associative organization and a block length of four 32-bit words. The cache is organized into 128 sets. There is a single “line valid bit” and three bits, B0, B1, and B2 (the “LRU” bits), per line. On a cache miss, the 80486 reads a 16-byte line from main memory in a bus memory read burst. Draw a simplified diagram of the cache and show how the different fields of the address are interpreted.

Answer:

Address Breakdown:

• Tag: 21 bits
• Set: 7 bits
• Word: 4 bits

Line Structure: Each cache line includes 21 bits of tag and a single “line valid bit” and 16 bytes of data. Note that only when the line valid bit is 1, the content of the line is valid. Each set includes 3 LRU bits and 4 lines. (4 ways for 4 lines)

Question 4.8:Consider a machine with a byte addressable main memory of 64K bytes and block size of 8 bytes. Assume that a direct-mapped cache consisting of 32 lines is used with the machine. Answer the following questions:

• How is a 16-bit memory address divided into tag, line, and byte number?
• Into what line would bytes with each of the following addresses be stored in the cache?
  • 0001 0001 0001 1011
  • 1100 0011 0011 0100
  • 1101 0000 0001 1101
  • 1010 1010 1010 1010
• Suppose the byte with address 0001 1010 0001 1010 is stored in the cache, what are the addresses of other bytes stored along with it in the cache?
• How many total bytes of memory can be stored in the cache?
• Why is the tag also stored in the cache?

Answer:

Question A:The 16-bit memory address is divided into tag, line, and byte number as follows:

• Tag: 8 bits
• Line: 5 bits
• Byte: 3 bits

Question B:The bytes with the given addresses would be stored in the following lines in the cache:

• 0001 0001 0001 1011: Line 3
• 1100 0011 0011 0100: Line 6
• 1101 0000 0001 1101: Line 3
• 1010 1010 1010 1010: Line 21

Question C:The byte with address 0001 1010 0001 1010 is stored in the cache, and the other bytes stored along with it in the cache are:

• 0001 1010 0001 1000
• 0001 1010 0001 1001
• 0001 1010 0001 1010(self)
• 0001 1010 0001 1011
• 0001 1010 0001 1100
• 0001 1010 0001 1101
• 0001 1010 0001 1110
• 0001 1010 0001 1111

Question D:The total number of bytes that can be stored in the cache is:

\[\text{Total Bytes} = \text{Number of Lines} \times \text{Line Size}\]

In this case, the number of lines is 32, and the line size is 8 bytes. Therefore, the total number of bytes that can be stored in the cache is:

\[32 \times 8 = 256 \text{ bytes}\]

Question E: The tag is also stored in the cache, for distinguishing between different blocks that are mapped to the same cache line.

Question 4.11: Consider a memory system with a 32-bit address to address at the byte level,plus a cache using 64-byte line size. Answer the following questions:

• Assume a direct-mapped cache with 20 bits of tag. Show the address format and determine params:
  • Number of Addressable Units
  • Number of blocks in main memory
  • Number of cache lines
  • Size of tag
• Assume an associative cache. Show the address format and determine params:
  • Number of Addressable Units
  • Number of blocks in main memory
  • Number of cache lines
  • Size of tag
• Assume an four-way set associative cache with 9 bits of tag. Show the address format and determine params:
  • Number of Addressable Units
  • Number of blocks in main memory
  • Number of lines in a set
  • Number of cache lines
  • Number of sets
  • Size of tag

Answer:

Question A:

• Address format: Tag[20] | Line[6] | Byte[6]
• Number of Addressable Units: \(2^{20+6+6} = 2^{32}\)
• Number of blocks in main memory: \(2^{26}\)
• Number of cache lines: 64
• Size of tag: 20 bits

Question B:

• Address format: Tag[26]| Word[6]
• Number of Addressable Units: \(2^{26+6} = 2^{32}\)
• Number of blocks in main memory: \(2^{26}\)
• Number of cache lines: undetermined
• Size of tag: 26 bits

Question C:

• Address format: Tag[9] | Set[17] | Word[6]
• Number of Addressable Units: \(2^{9+17+6} = 2^{32}\)
• Number of blocks in main memory: \(2^{26}\)
• Number of lines in a set: 4
• Number of cache lines: 524288
• Number of sets: 131072
• Size of tag: 9 bits

Question 4.22: A computer has a cache, main memory, and a disk used for virtual memory. If a referenced word is in the cache, 20ns are required to access it. If it is in main memory, it requires 60ns to load it into the cache, and then the reference is started again. If the word is not even in the main memory, 12ms is needed to fetch the word from disk to main memory. The cache hit ratio is 0.9 and the main memory hit ratio is 0.6. What is the average time in ns required to access a referenced word on the system?

Answer:

Cache hit: 0.9×20=18 ns

Cache miss, main memory hit: 0.1×0.6×80=4.8 ns

Cache miss, main memory miss: 0.1×0.4×12,000,080=480,003.2 ns

Overall: 480026 ns.