这一章是在DSP整体框架下，讨论Nyquist采样定理，欠采样、升采样的引入以及整数M倍抽取和L倍内插的采样方法。要求会画信号抽取前后的频谱，并掌握分析信号是否混叠的办法。

Summary for DSP Chapter 2

Flowchart for DSP

数字信号转化为模拟信号的步骤为：采样、保持、量化、编码。这一部分实际上是反映了A/D模块，或者采样器的功能。而对于D/A模块，则需要对数字信号进行内插后进行平滑滤波，才能得到模拟信号。下面给出了一个流程图供参考。
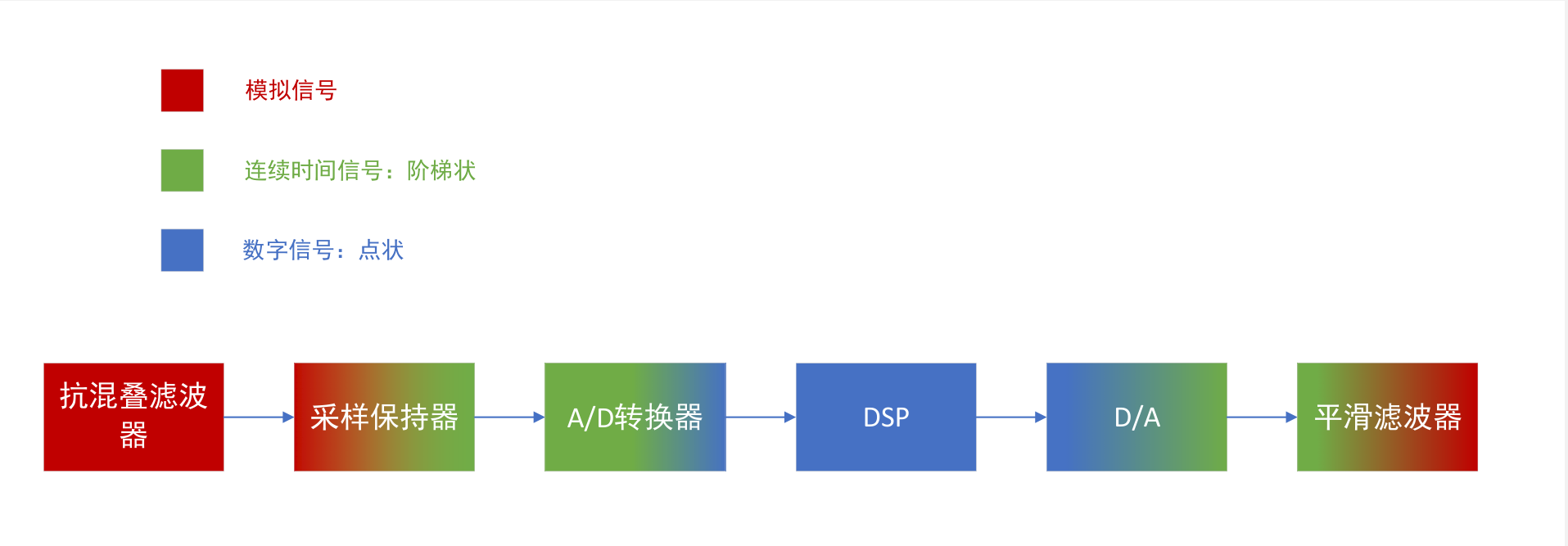
DSP flowchart

本章的其余内容主要围绕模拟信号与连续数字信号之间转换的器件、方法展开。数字信号的部分是第三章之后的内容。

对于等间隔采样，拥有采样周期 \(T\)，对应的采样频率为\(f_s\)，对应的角频率为\(\Omega_s = 2\pi f_s\)。

因此，在画频谱图时，\(\Omega\)是经过采样后，信号实际的角频率。而\(\omega\)则是归一化到\(2\pi\)后的角频率，即\(\omega = \frac{\Omega}{f_s}\)。

采样的过程就是时域信号与周期冲激信号的乘积，其频谱为原信号频谱的周期延拓。如果信号的频谱最高超过了\(\frac{\Omega_s}{2}\)，就会出现混叠。

主要了解两种滤波器：

对于抗混叠滤波器，一般是提高采样频率以增加过渡带宽，然而此时A/D转换器的采样数据量会增加。对于平滑滤波器，其理想特性是和零阶保持器紧密相关。该保持器要求冲激响应为一个长度为\(T\)，高度为1的门函数。

如果是带通信号，其在直流和最低频谱之间的大量频带值为0。因此，如果在这些频率上的值被混叠了，带通信号只需要通过一个带通滤波器仍然可以重建。这种技术叫做欠采样。因此，对于采样频率\(\Omega_s\)的限制就大幅度降低了。

欠采样的操作方法
1. 扩展带宽，使得带通信号的最高频率\(\Omega_2\)是改动后带宽的整数倍。令这个倍数为\(M\)。
2. 采样频率\(\Omega_s\)的计算：\(\Omega_s = \frac{2\Omega_2}{M}\)。
3. 带通滤波器滤波。

离散时间信号主要使用“整数M倍抽取”和“整数L倍内插”作为采样和插值的方法。对于离散信号的采样，实际上是抽取过程，相当于降采样。对于离散信号的插值，实际上是内插过程，相当于升采样。注意实际应用中一定是先升采样再降采样。

经过整数M倍抽取后，新的采样频率为\(f_s/M\)，此时基带频率拓宽为原来的M倍。

经过整数L倍内插后，新的采样频率为\(f_s\times L\)。此时基带频率缩减为原来的\(\frac{1}{L}\)。内插的方法为在离散信号的两个点之间插入L-1个0，然后抗镜像滤波（LPF），取频率范围(0,\(\frac{\pi}{L}\))得基带信号。

这种题一般会直接给出离散时间信号的频谱，要求画出不同抽取倍速抽取后的频谱。我们以\(\omega\)作为横坐标，\(X(e^{j\omega})\)作为纵坐标的情况讨论。实际情况中，横轴可能改为\(\Omega\)。

展开，画出\(-2M\pi\)到\(2M\pi\)的抽取信号频谱。抽取过的信号占据的角频率范围为\(M \times BW\)，依据这个画出两边的频谱。注意幅度为1/M
对最左侧的单个谐波频谱分量，依次向右平移\(2\pi\)，复制直到与右侧重合。注意在画的时候，该信号的频谱一定是关于y轴对称的。

讨论的情况和之前的相同。此时相当于将原来\(±2\pi\)、\(±4\pi\)等谐波分量镜像到\((-\pi,\pi)\)中。抽取过的信号占据的角频率范围为\(\frac {BW}{L}\)。注意幅度为L倍

Tags: Digital Signal Processing