Note: 本文内容主要基于《通信电子线路》第二章内容整理,主要介绍了选频网络和阻抗变换。
信号的选频滤波
选频滤波器的分类
大体上,选频滤波器可以分为下面的几个大类。
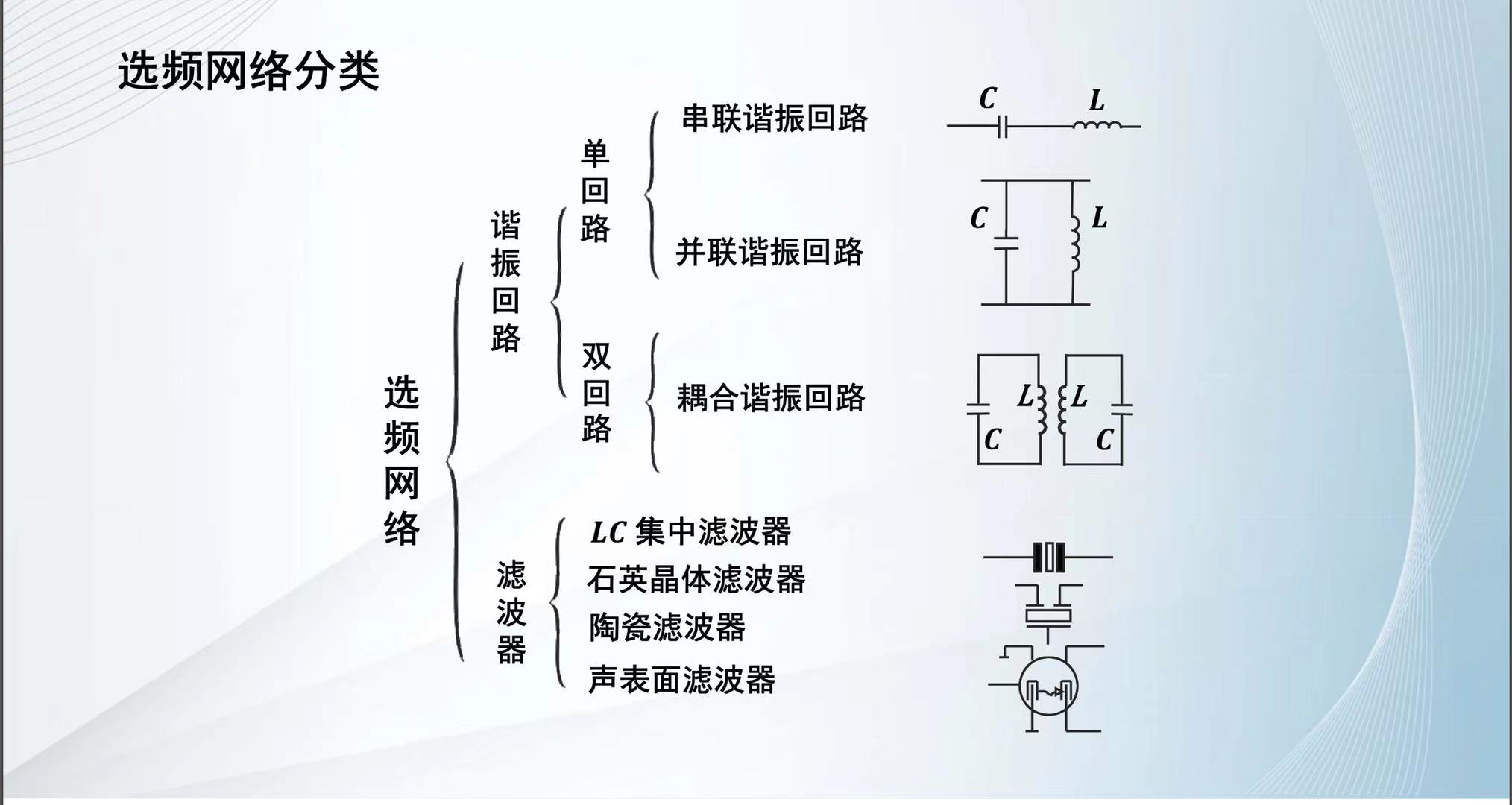
同时,按照实现功能,又可以分为:
- 预选滤波器
- 中频通道滤波器
选频滤波器的主要参数计算
选频滤波器的主要参数有:
- 频率特性 & 品质因数
- 带宽
- 波形因数\(SF = \frac{BW_{-60dB}}{BW_{-3dB}}\)
- 输入输出阻抗(阻抗匹配)
频率特性相关参数
所有的参数都围绕着\(\omega\)展开。
- 品质因数: 分为空载品质因数(\(Q_0\))和带载品质因数(\(Q_P\))。前者不带信号源和负载,后者带信号源和负载。它的物理意义是谐振时特性阻抗和电阻的比值。
- 幅频响应:\(A(\omega)\),即信号在不同频率下的幅度响应。
- 相位响应:\(\phi(\omega) =- \arctan \xi\),即信号在不同频率下的相位响应。
- 和品质因数、选择性的关系:Q 值越大,在谐振频率附近相位下降越快,滤波器线性范围变差,但选择性会变好。
算带宽 BW 和选择性(波形因数)SF
在“失谐”时,阻抗不匹配,此时从幅频响应上能看出来,会出现一个带宽。
\(BW =\frac{f_0}{Q_0}\)(Hz)
这里有一个十分神奇的计算方法,可以将 3dB 带宽直接和品质因数联系起来,计算 LC 滤波器的带宽。详细的推导过程见Q0 是怎么和频率/带宽扯上关系的呢?。然而对于选择性 SF,就需要带电路参数进行计算了,因为涉及-60dB 带宽的计算。
60dB 衰减,即幅度衰减 1000 倍,我们代入LC 滤波器的幅频响应:
\[A(\omega) = \frac{1}{\sqrt{1+Q_P^2(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega})^2}}\]就可以找到两个\(\omega\),进而算出带宽。这是带宽的通用算法。当然,这是乘了\(2\pi\)的结果,实际结果还需要归一化。
阻抗匹配
在这里,我们主要讨论两种匹配回路:L 型匹配回路和传输线变压器阻抗变换。
L 型匹配回路
它的物理意义就是,对于一个选频网络,我需要通过补偿电容 or 电感,使得谐振频率和工作频率相同。
对于这种题的求解,需要确定信号源和负载的大小关系,然后分情况带公式。最关键的是算出不同情况下的\(Q_e\),以及感性、容性阻抗算法的区分。
- \(Q_e\)的计算公式:
- 算阻抗
- 对于感性阻抗: \(X =Q_e\cdot R\)
- 对于容性阻抗: \(X = \frac{R}{Q_e}\)
注意题目中如果给出某电感/电容,以及它们的参数(如品质因数\(Q_0\)),则需要根据阻抗匹配结果减去它们的值。
- 回路效率:\(\eta = \frac{P_L}{P_i}\)
- (存疑)对于并联 L 型匹配回路,\(\eta = \frac{P_L}{P_i} = \frac{R_L}{R_L+R_S}\)。
- 滤波度(带外抑制因子):\(\varphi_n = \frac{n}{Q_e(n^2-1)}\)
- 带宽:\(BW = \frac{f_0}{Q_e}\)
传输线变压器阻抗变换
传输线变压器是绕在磁环上的射频传输线构成的变压器,经常用多股双绞线连接。它的上限频率取决于传输线长度,下限频率取决于初级绕组电感量。
重点求以下两个参数:
- 特征阻抗: \(Z_C = \frac{v}{i}\),一般先求解出\(R_L(v,i)\),再求解出\(Z_C\)。
- 阻抗变换关系: \(\frac{R_i}{R_L}\)
有三种基本的传输线变压器,分别是:
- 1:1 倒相变压器
- 4:1 传输变压器(输出线正极接到输入端负极),特征阻抗\(Z_C = 2R_L\)
- 1:4 传输变压器(输出线负极接到输入端正极),特征阻抗\(Z_C = 0.5R_L\) 名称中的比例代表阻抗变换关系。
依照这三种基本的传输线变压器,可以变化出多种阻抗变换关系。基本的分析思路是假定输入端电压为\(v\),输入端电流为\(i\),然后参考这些基础变压器的阻抗关系,求解输出端电压和电流,进而求解出阻抗变换关系。有点像模电里面的镜像电流源。